在这节课中，我们将学习旅行问题中一些更全面的主题。
为此，我们需要复习我们所学的基本数量关系:距离=速度×时间； 总距离=速度和x时间； 距离差=速度差×跟踪时间
例1小华在8点到9点之间开始解决一个问题，当时时针和分针在一条直线上，当问题解决后，两个指针第一次重合。问题:小明花了多长时间解决这个问题？
分析:这个问题实际上是一个旅行问题。开始时，两根针在一条线上，最后，两根针第一次重叠。因此，在我们观察的时间段内，两个针之间的距离差是30分贝，并且因为时针以每小时5分贝的速度行进，即其速度是1/12分贝/分钟，而分针的速度是1分贝/分钟。因此，当它们第一次重合时，分针必须从后面赶上时针。这是一个追踪问题。追踪时间是小明解决问题的时间。解决方案:30 ÷ 1-1/12)=30 ÷ 11/12=32和8/11(分钟)例2 A、2B和C以每分钟60米的速度行走，B以每分钟50米的速度行走，C以每分钟40米的速度行走。甲从甲地开始，乙和丙同时从乙地开始，向对方走去。相遇后，15分钟后，甲、乙与丙再次相遇，找出甲、乙之间的距离图纸如下: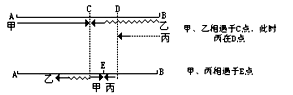
分析:结合上图，如果我们假设甲、乙在丙点相遇，丙在丁点，那么因为甲、丙在15分钟后在戊点相遇，丙与丁之间的距离等于(40 60) × 15=1500(米)。也因为b和c同时从b点出发，在同一时间，b走到c点，c走到d点，也就是说，b同时比c多走1500米，b和c的速度差是50-40=10(米/分钟),因此b到c的时间是1500 \u 10=150(分钟),也就是说，a和b到c的时间分别是150分钟，因此，a和c之间的距离例3 A、B和C是同一条路上的三个车站。从B到A和C的距离相等。萧蔷和小明同时分别从A和C出发。萧蔷和小明在经过100米的时候相遇了。然后他们继续前进。萧蔷去了c后马上回来，经过300米时，他追上了小明，问道:A和B之间的距离是多少？
先画下图: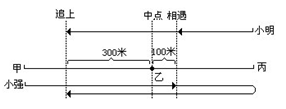
分析:结合上图，我们可以将上述动作分为两个阶段来考察:情况5A和B分别同时从A和B开始。如果两者朝着同一个方向，甲将在26分钟内赶上乙；如果两个人走向对方，他们可以在6分钟内见面。众所周知，乙每分钟行驶50米，甲和乙之间的距离是计算出来的。
先画下图: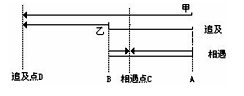
分析:如果甲和乙相遇的地方是丙，甲和乙相遇的地方是丁，甲到丙需要6分钟，甲到丁需要26分钟。因此，当甲走丙和丁之间的距离时，需要的时间应该是(26-6)=20(分钟)。解决方案:50×(26±6)> 26-6)=50×32 \u 20=80(m/min)(80±50)×6=130×6=780(m)
甲:甲和乙之间的距离是780米。同时，从上图可以看出，C和D之间的距离等于BC加BD。也就是说，B在6分钟内行驶的距离与26分钟内行驶的距离之和是50×(26 ^ 6)=1600(米)。因此，A的速度是1600 ÷ 20=80(米/分钟)，这样就可以得到A和B之间的距离。
例6在高速公路上，有一个骑自行车的人和一个行人。骑车人的速度是行人的三倍。每6分钟，一辆公共汽车超过行人。每10分钟，一辆公共汽车超过骑自行车的人。如果公共汽车出发站的出发时间间隔保持不变，那么每隔几分钟就会有一辆公共汽车来？
分析:对于汽车的出发时间间隔，只需要找出汽车的速度和相邻两辆汽车之间的距离，但这个话题并没有直接告诉我们这两个条件。如何找到这两个量？
解决方法:相邻两车之间的距离(以下简称分离距离)是恒定的。当一辆公共汽车经过行人时，下一辆公共汽车和行人之间的距离就是分离距离。每6分钟就有一辆车经过行人。也就是说，当一辆车经过行人时，下一辆车需要6分钟才能赶上行人。汽车和行人之间的距离差是两个相邻汽车之间的间隔距离。
同样的分析也适用于骑自行车的人。因此，如果我们把汽车的速度当作V，骑车人的速度是V，行人的速度是V(米/分钟)，那么:
间隔=(V -V) ×6(米)，间隔=(V -V) ×10(米)，V=3V。
综合以上三个公式，我们可以得到:V=6V，即V=1/6V，那么:区间=(V -1/6V) * 6=5V (m)
因此，车辆的发车时间区间等于:区间\v=5V(m)V(m/min)=5(min)。
例7A和B正以相同的速度沿着铁路走向对方。一列火车在8秒钟内经过甲，离开甲5分钟后遇到乙，7秒钟后经过乙。B和火车相遇几分钟后，他们又相遇了。
分析要求当甲和乙相遇几分钟后，甲和乙的距离和他们的速度之间的关系必须被找到。与此相关的是火车的运动。只有通过火车的运动才能找到甲和乙的距离。列车的运行时间是已知的，因此必须找到它的速度，并且至少必须找到它与A和B的速度之间的比例关系。由于这个问题的难度，一步一步的详细解释如下:
做习题
点击查看小学数学思维训练主题数据库，阅读更多相关文章！
①找出甲方和乙方的列车速度v和速度v之间的关系，如果列车长度为l，则: (一)列车经过甲方一侧需要8秒钟。这个过程是一个后续问题:因此，L=(车辆-车辆人)×8；(1) (二)列车经过b需要7秒钟。这个过程是一个会议问题:因此，l=(V车，V人)×7。(2) 从(1)和(2): 8(V -V)=7 (V-V)，因此，V-V=l5V。 (2)机车与a相遇的地方与机车与b相遇的地方之间的距离为:(8 5×6O)×(V车V)=308×16V=4928V (3)当机车遇到b时，找出a和b之间的距离。 机车遇到a后，机车需要(8±5×60)秒才能遇到b，因此当机车遇到b时，a和b之间的距离为4，928v-2(8±5×60)v=4，312 v。 (4)请甲乙双方几分钟后见面？4312伏人÷2V人=2156(秒)=35和28/30分钟
